2019.11.15

Quaternion を完全に理解した

こんにちは、開発者の t-kuhn です。Unity Engine に携わる仕事をすると必ず Quaternion に遭遇します。何だか不思議な名前で数学概念はとっつきにくいから「とりあえず回転を表すモノ」と脳内保存して次に進む開発者も多いでしょう。この記事では Quaternion * Quaternion と Quaternion * Vector3 がどのような場面で使われるか、また簡単な例をもとに計算自体はどうなっているかについて書きたいと思います。

// Unity Engine の Quaternion のコンストラクター
// Quaternion は4つの要素（x, y, z, w）からできています。
public Quaternion(float x, float y, float z, float w)
{
    this.x = x;
    this.y = y;
    this.z = z;
    this.w = w;
}

// Unity Engine の Quaternion のコンストラクター

// Quaternion は4つの要素（x, y, z, w）からできています。

public Quaternion(float x, float y, float z, float w)

{

this.x = x;

this.y = y;

this.z = z;

this.w = w;

}

ある日、Quaternion クラスが * の operator overload を定義していることに興味を惹かれた。この operator overload が定義されているから C# で Quaternion * Quaternion と Vector3 * Quaternion のコードが書けるようになる。これからそれぞれの動作を確認してから実際の計算を追っていきたいと思います。

Quaternion * Quaternion

まずは2つの Quaternion q1 と q2 の掛け算について考えよう。交換法則が成り立たないから

と書ける。成り立たないから基本的には（例外はある） q1 * q2 と q2 * q1 を計算した結果が異なるはずです。確認しよう。

q1 * q2

まず q1 * q2 です。

// q1 * q2
// rotate around y-axis first and then tilt up around the rotated z-axis.
var q1 = Quaternion.Euler(0f, Time.time * 50f, 0f);
var q2 = Quaternion.Euler(0f, 0f, -45f);
var q = q1 * q2;
_grayVector.transform.rotation = q;

// q1 * q2

// rotate around y-axis first and then tilt up around the rotated z-axis.

var q1 = Quaternion.Euler(0f, Time.time * 50f, 0f);

var q2 = Quaternion.Euler(0f, 0f, -45f);

var q = q1 * q2;

_grayVector.transform.rotation = q;

このコードを実行したら _grayVector はどのように動くでしょうか？それを知るためにはまず _grayVector の回転されていないときの様子を確認する必要がある。

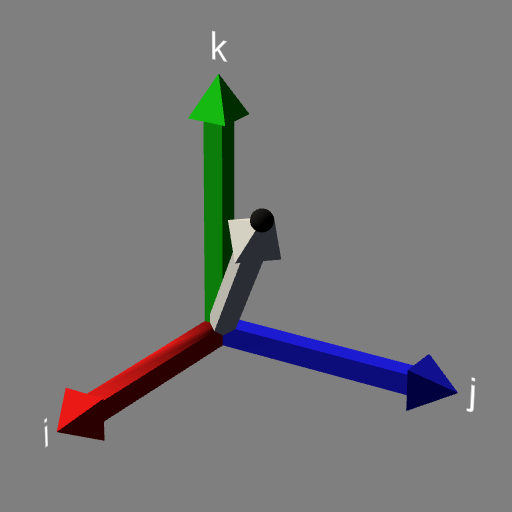
この図の _grayVector が _grayVector.transform.rotation = Quaternion.Identity のときの _grayVector です。赤、緑、青の矢印が長さ 1 の世界座標だとすると _greyVector の終点はちょうど (-1f, 0f, 0f) を指していることが分かる。

さてコードを実行しよう。

まずここで分かるのは grayVector の原点が世界座標の原点と同じ位置になっていることです。原点がもし矢印メッシュの中心になっていたらこのような回り方はしないです。

q1 と q2 の中身を見よう：

q1 ：時間が経つとともに y-axis を回転軸に回る
q2 ：z-axis を回転軸に -45° 回る

後、 q1 * q2 なので最終的な回転 q は q1 が適用された後に q2 を適用したときの結果と考えることができる。ここで非常に重要なのは q1 を適用した後のそれぞれ回転軸は q1 の回転分だけ一緒に回る ということです。一緒に回転するから q2 の回転軸である z-axis は毎フレーム少しずつ y-axis を回転軸に回っています。

q2 * q1

さて、順番を逆にしたときの結果を調べましょう。以下のコードは q = q2 * q1; のところ（ここを逆にした）以外上のコードと同じです。

// q2 * q1
// tilt up first and then rotate around the now tilted y-axis
var q1 = Quaternion.Euler(0f, Time.time * 50f, 0f);
var q2 = Quaternion.Euler(0f, 0f, -45f);
 var q = q2 * q1;
_grayVector.transform.rotation = q;

// q2 * q1

// tilt up first and then rotate around the now tilted y-axis

var q1 = Quaternion.Euler(0f, Time.time * 50f, 0f);

var q2 = Quaternion.Euler(0f, 0f, -45f);

var q = q2 * q1;

_grayVector.transform.rotation = q;

コードを実行した結果はこれです。

今度は「z-axis を回転軸に -45° 回る」を適用してから「時間が経つとともに y-axis を回転軸に回る」。回転されていない状態（この状態だと世界座標が回転軸と一致する）から z-axis を回転軸に -45° 回ると y-axis が一緒に回って傾いた状態で止まります。この傾いた y-axis を回転軸にさらに「時間が経つとともに回る」から上図のようになります。

Quaternion * Vector

Quaternion の掛け算で様々な回転を組み合わせることができることを確認してきました。次は Quaternion * Vector の動作確認ですが、これは任意のベクトルを任意の Quaternion で回転させるための operator overload で戻り値は Vector3 になります。

Vector3 なので今度は (-1f, 0f, 0f) に配置された黒い球を考えよう。_grayVector の終点もちょうどこの位置を指しているから残しておくことにした。

// Quaternion * Vector3
var q = Quaternion.Euler(new Vector3(0f, Time.time * 50f, -45f));
var p = new Vector3(-1f, 0f, 0f);
var pDash = q * p;
_grayVector.transform.rotation = q;
_blackBall.transform.position = pDash;

// Quaternion * Vector3

var q = Quaternion.Euler(new Vector3(0f, Time.time * 50f, -45f));

var p = new Vector3(-1f, 0f, 0f);

var pDash = q * p;

_grayVector.transform.rotation = q;

_blackBall.transform.position = pDash;

上記のコードを実行すると

無事黒い球を q で回転させることに成功しました。

なんでそれで動くの？

これでやっと前置きが終わり、私が本当に書きたかったところまで来た。「何でこの operator overload でこんな結果になるか？」について書きたかったのです。つまり、なんで Quaternion * Quaternion というコードを書くとそれらの回転を組み合わせた Quaternion が生まれるか。そして、何で Quaternion * Vector3 というコードを書くと Quaternion 分回転された Vector3 が得られるか。

つまり、ブラックボックスになっているそれらの計算の正体についてこれから書きたいと思います。

Quaternion * Quaternion の正体

// q1 * q2
// rotate around y-axis first and then tilt up around the rotated z-axis.
var q1 = Quaternion.Euler(0f, 135f, 0f);
var q2 = Quaternion.Euler(0f, 0f, -45f);
var q = q1 * q2;
_grayVector.transform.rotation = q;

// q1 * q2

// rotate around y-axis first and then tilt up around the rotated z-axis.

var q1 = Quaternion.Euler(0f, 135f, 0f);

var q2 = Quaternion.Euler(0f, 0f, -45f);

var q = q1 * q2;

_grayVector.transform.rotation = q;

このコードで何が起きているでしょうか？コードを実行したら以下の結果になりますが、私たちが求めているのはそこではない。

Unity に全てを計算してもらうと Quaternion q に格納される値は次の通りです。

q1 * q2 を計算して同じ結果になるかどうかを確認すればいいが、まずは (1.2) を少し書き換えます。Unity Engine は Quaternion のそれぞれの成分を実数で表現していますが、計算結果が合っているかどうかの比較がしやすくなるように実数を三角関数に置き換えます。こういうときは Wolfram Alpha が便利です。

次に q1 と q2 の値を見よう。上と同じようにそれぞれの要素を三角関数で表すと q1 は

で q2 は

となります。

ここで一度 Quaternion を数学的にどのように表現するかについて書いておこう。q1 を次のように書きます

Quaternion は4次元ベクトルです。スカラーと区別が付くように q1 は太文字になっています（ベクトル＝太文字という約束です）。i, j, k がついている要素を Quaternion の複素成分、s1 を Quaternion のスカラー成分として考えることができる。

q1 をベクトル表記で表すと

となります。また、3つの複素成分を一つの3次元ベクトルにまとめて書くと

となります。

Quaternion の掛け算に進む前に Quaternion の基本式を表記しなければならない。この基本式は Quaternion を考え付いた Sir William Rowan Hamilton が発見したもので Quaternion 数学の基礎になっています。

これで Quaternion の掛け算に必要なものが揃っています。

(1.10) の右辺を分配法則に従って展開し、そして (1.9) を適用すると

が得られます。 (1.11) の q1 と q2 に (1.4) と (1.5) を代入すればこれで q が求まるが、項が16個もあるから、少し整理してみましょう。整理するためにベクトルの外積と内積が必要になるからここに書いておきます。

(1.12), (1.13) より、(1.11) の右辺の項を次のように整理できます。

さて、 (1.14) に (1.4), (1.5) を代入して (1.5) と同じ結果が得られるかどうかを確認しよう。

まず (1.4) をベクトル表記で表すと

が得られます。同様に (1.5) より

(1.15) ~ (1.18) を (1.14) に代入して計算すると

と q が求まり (1.3) と比較すると Unity Engine と同じ結果が得られたことが分かります。やったぜ！何も数学的に証明したわけではありませんが、簡単な例を通して Unity Engine が内部的に

と同等な数式で Quaternion * Quaternion を計算していると確信が持てるようになった。最後に (1.1) をもう一度見てみましょう。

Quaternion の掛け算では交換法則が成り立たないと上に書きましたが、 (1.14) を見ると「あぁ、確かに、こりゃ交換法則が成り立たないねー」とその理由が分かる人もかなり多いのではないでしょうか（ヒント：外積）。

Quaternion * Vector3 の正体

単刀直入に書きますと Unity Engine の Quaternion * Vector3 の計算の正体は

です。ここで、 p は回したいベクトルで、 p' は回した後に得られたベクトルです。 q はもちろん Quaternion です。

さて、前章と同じふうに Unity Engine と自力で計算した結果が一致するかどうかを確認することによって Unity Engine が内部的にやっている計算が (1.22) と同等であるかどうかを確認したいと思います。

黒い球の位置ベクトルを前章求めた q で回転させよう。上図に回転を適用する前の状態を示す。

そしてこれが回転を適用した後の状態です。 Unity Engine では Quaternion クラスが定義している * operator overload を利用して

var q = Quaternion.Euler(new Vector3(0f, 135f, -45f));
var p = new Vector3(-1f, 0f, 0f);
var pDash = q * p;

var q = Quaternion.Euler(new Vector3(0f, 135f, -45f));

var p = new Vector3(-1f, 0f, 0f);

var pDash = q * p;

と書けますが、実際の計算は q * p ではなくて

です。回転前のベクトル p は

になります。そして、Unity Engine で計算した結果、回転後のベクトル p' は

です。さて、 (1.22) に (1.23), (1.21) を代入し自力で計算するターンです。

まず、 q の逆行列 q^-1 を計算しておきます。

(1.22) の計算を二つに分けます。

(1.26) を計算してから (1.27) を計算すれば p' が求まります。掛け算のやりかたは Quaternion * Quaternion と一緒ですが、 p を4次元ベクトルに拡張する必要があることに注意。

前章で求まった q をもう一度書いておきます。

次に4次元ベクトルに拡張された p を書いておきます。

0の要素が3つもあるのは計算が楽になるから嬉しいですね。

これで (1.26) の計算ができました。次に (1.27) の計算に進みます。 (1.26) と同様に、定義からいきます。

そして前と同様に計算していくと

と p' が求まります。 Unity Engine が計算した値 (1.24) と比較すると一致していることが分かる！最後の最後にすごい量になりましたが、計算が合っているようです。

この計算を通して Unity Engine で Quaternion * Vector3 を書くと内部的に行われるのが

に相当する処理であることに確信が持てるようになりました。

リンク集

Category
t-kuhn /
技術